引言
热力学的确是一门很神奇的学科。从亿万年前动物的远祖进化出冷热感知,到远古时代人类与火的邂逅,到文艺复兴之后燃素说、热质说的兴起与崩溃,再到经典热力学大厦的落成,最后到非平衡态热力学如同新星般冉冉升起,热力学始终陪伴着人类的历史。虽然在名义上是物理学的分支,但它的触角早已遍布科学的各个领域。诸如传热学、化学热力学之类的学科都不过是这个庞大帝国的一方诸侯罢了。
在互联网如此发达的今天,热力学中的许多概念已经深入人心。能量守恒早已成为所有人的常识(一些民科除外),更别提那个常年在各路科普中叱咤风云的“熵”,还有在各种科幻作品中反复提及的“宇宙热寂”。它们到底是什么?有人由此断言人类文明,甚至是整个宇宙都终将灭亡;但也有人说,生命因为熵增而产生。这些论断究竟可不可信?
在这篇文章中,我将用并不高深的数学方法和一系列思想实验,从人们对于世界的最初认知开始,一步步推导到宇宙的热寂。由于本人实力有限,如果在什么地方出现了错误,或者什么地方觉得看不懂,请在评论区中留言。
正文
序章一:理想气体与低压气体定律
$1621$ 年,近代化学的奠基人波义耳($R.~Boyle$)在研究气体时提出了波义耳定律。该定律指出,一定量气体在温度不变时,其体积与压力成反比。即:
\[p\propto\frac{1}{V}\]后续的科学家重复他的实验,却发现这个定律总是“时灵时不灵”。总结实验数据,人们发现气体只在低压时比较符合规律,而如果气压大于 $\text{1MPa}$ 便不再符合。波义耳定律作为第一个定量描述气体的公式,启发了人们继续探索低压时气体物理量之间的关系。
$1787$ 年,法国物理学家查理($J.~A.~C.~Charles$)在研究低压气体的膨胀时发现,一定量气体在压力恒定时,其体积与温度成正比。但不知为何,查理并没有发表这一规律。$15$ 年后,法国科学家盖·吕萨克($J.~L.~Gay\text{-}Lussac$)偶然得知了查理的这一发现,并在重复实验后将其发表。因此,该定律也被称为查理-盖·吕萨克定律:
\[V\propto T\]把时间拨回 $1787$ 年,查理当时在研究低压气体时还有一项发现,即一定量气体体积一定时,其压强与温度成正比。是为查理定律:
\[p\propto T\]$9$ 年之后的 $1811$ 年,意大利化学家阿伏伽德罗($A.~Avogadro$)指出,在温度、压力不变时,相同体积的不同气体含有相同的分子数,且体积与分子数成正比。后来,人们将这条规则其称为阿伏伽德罗定律:
\[V\propto n\]$1834$ 年,法国工程师克拉伯龙($B.~P.~E.~Clapeyron$)综合上述定律,得到了著名了克拉伯龙方程。由于严格的推导需要用到偏微分,而这个方程的推导并不是我们的重点,所以此处只给出一个不严谨但非常简单的推导过程。
将阿伏伽德罗定律 $V=C_{4}n$ 代入波义耳定律 $pV=C_1$,得到 $C_4pn=C_1$;将查理定律 $p=C_3T$ 代入,可得
\[C_3C_4Tn=C_1\]再次代入波义耳定律 $pV=C_1$,得到
\[C_3C_4Tn=pV\]即 $Tn\propto pV$。写成我们常用的形式,即是 $pV=nRT$。后来,人们抛弃了“低压气体”这种不严谨的说法,而是将在任何温度、压力下都严格符合克拉伯龙方程(还有之后会讲到的焦耳定律)的气体定义成了一个抽象的概念,即理想气体(因此克拉伯龙方程也被称为理想气体状态方程)。之所以说它抽象,是因为在物理学深入微观之后,人们发现这种气体在现实中不可能存在,而仅存在于我们的思考和想象中。
但是,抽象的概念往往更逼近事物的本质,我们很快就会在一系列思维游戏中见识到它的威力。不过在此之前,还有一些事不得不提,那就是——能量守恒。
序章二:热力学第一定律和焦耳实验
$1770$ 年,氧气的发现者,英国化学家普利斯特里($J.~Priestley$)提出热质说,认为“热”是一种气态物质,其他物质吸收了“热”,温度就会升高;放出“热”,稳定度就会降低。在 $1772$ 年,近代化学之父拉瓦锡($A.~de~Lavoisier$)用实验否定了统治科学界几百年的燃素学说之后,热质说即开始盛行。它的确能解释关于热的很多问题,但既然是一种物质,便不会凭空创生或毁灭,因此热质说也被称为“热守恒理论”。这个时候如果有人开上帝视角,就会发现“热守恒”与我们今天认可的“能量守恒”是相悖的,即热和其他能量间可以相互转化。
$18$ 世纪末,美国工程师伦弗特($C.~Lunford$)和英国化学家戴维($H.~Davy$)的实验让热质说受到了猛烈的冲击。戴维在真空环境中摩擦两个冰块,结果冰块融化,并由此认为热是一种能量而非物质。$19$ 世纪初,热力学的奠基人之一卡诺($N.~L.~S.~Carnot$)首次提出了热功转换,但他只是在给热质说的旧框架缝补,所以并没有掀起太大的波澜。$19$ 世纪 $50$ 年代,焦耳($J.~P.~Joule$)、迈尔($J.~R.~Mayer$)、亥姆霍兹($H.~von~Helmholtz$)三人分别从实验、哲学和数学角度导出了能量守恒定律,但都遭到了旧派学者极其猛烈的攻击。
直到 $1850$ 年,克劳修斯($R.~J.~E.~Clausius$)与兰金($Z.~Rankine$)总结了前人的工作,正式提出“能量守恒”应该作为热力学的首要定律。凭借着在学界多年积攒的影响力,克劳修斯等人舌战群儒,最终驳倒了保守派。克劳修斯的胜利被视为经典热力学的正式诞生,而能量守恒也从此深入人心。
克劳修斯对热力学第一定律是这样表述的:能量既不会凭空产生,也不会凭空消失,它只会从一种形式转化为另一种形式,或者从一些物体转移到另一些物体,而其总量保持不变。他也提出了该定律的数学表达式:
\[\Delta U=Q+W\]上式对于一切宏观的封闭系统都成立。所谓封闭系统,是指一个与外界没有物质交换的系统,但它允许能量的交换。想象一下,我现在有一种可以完全阻止任何物质穿过且坚不可摧的理想材料,我用它做一个碗,那么碗的内部不可以看成一个封闭系统,因为你可以通过碗口把东西放进去,当然也可以把东西拿出来。但如果我用这种材料做一个球,那球的内部就可以看成封闭系统,因为这种材料能够完全阻隔任何物质,你没有任何办法放进或拿出任何东西。当然,你可以把这个球架在火上烤,由于这种材料无法阻隔热,因此你可以向球内传递能量。当然,我知道现实中几乎不存在封闭系统(我们在文末会讨论为什么要加上“几乎”二字),但要记住,在思想实验中并不存在现实的问题。
看完了适用条件,再让我们看看表达式本身。等号右边的 $Q$ 表示系统吸收的热,而 $W$ 表示环境对系统做的功(在计算时一定要注意 $Q$ 和 $W$ 的方向,为避免混淆,我们在后面会规定二者的方向);等号左边的 $U$ 是克劳修斯定义的一个概念,表示系统内一切能量的总和,也就是内能。遗憾地说,我们很难给出系统内能的绝对值(质能方程什么的不在今天的讨论范围内),但我们一般只需要内能的变化值,也就是 $\Delta U$。
克劳修斯认为,虽然我们不知道内能的绝对值,但我们可以明确它与什么量有关。他认为,内能就是构成物质的小微粒的动能与势能之和,即 $U=E_k + E_p$。要注意,今天的我们知道在这些“小微粒”中,还有核能、电子运动能等形式的能量,但克劳修斯没有这个概念,它想象中的“小微粒”基于道尔顿的实心球模型,说白了就是一个不可再分的小球,因而只有动能和势能。今天的我们通常把这样定义出来的“内能”成为“狭义内能”或者“热力学能”,本文中为方便理解,所有的“内能”字眼都指狭义内能。
在那个年代,热质说被能量守恒判了死刑之后,热的运动说开始兴起,也就是认为热的本质是微粒的运动,而温度就代表了微粒运动的快慢。即,温度 $T$ 与微粒运动速度 $v$ 正相关;进一步,微粒动能 $E_k$ 与微粒运动速度 $v$ 正相关,那么显然内能 $U$ 便与 $T$ 正相关。克劳修斯进一步认定,对于一定量的理想气体来说,$U$ 只与 $T$ 有关,其他任何量都无法影响 $U$。而他说这句话的底气,就是著名的焦耳实验。
焦耳像下图中这样把两个连在一起的烧瓶浸没在水中,中间用阀门阻隔。左边的烧瓶中充满了某种有色气体,而右边的烧瓶抽真空。接着,把它们中间的阀门打开,左边烧瓶中的气体向真空扩散,最终充满右边的烧瓶。
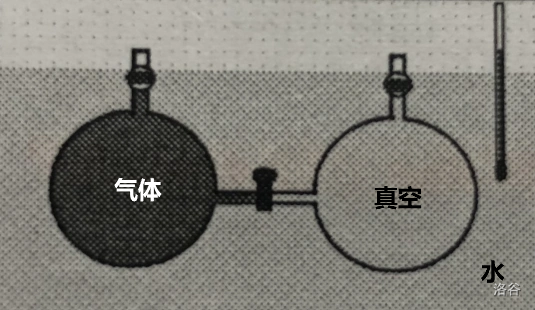
焦耳一边观察气体扩散,一边观察一支下端浸没于水中的温度计的示数。他发现,在气体扩散过程中,温度计示数没有变化。他依此认为,气体在向真空中膨胀的过程中不放热也不吸热。后来有人质疑,由于水的比热容太大了,即使有热交换也难以在温度计上发生肉眼可见的变化。再后来,一些科学家重新设计并拓展了焦耳的实验,得出结论:低压气体向真空膨胀时不吸热、不放热,且不做功。在理想气体概念出现出现后,人们把结论中的“低压气体”改成了“理想气体”。现在,克劳修斯要把这个结论代入到内能的研究中了。
因为 $\Delta U=Q+W$,而 $Q=0,W=0$,所以 $\Delta U=0$。在这一过程中,气体的气压 $p$、体积 $V$ 都发生了变化,但内能并没有变,进而 $U$ 与 $p,V$ 无关;理想气体的其他物理量要么在逻辑上与微粒运动没有关系,要么可以用 $p,V,T$ 导出,因此克劳修斯认定:一定量理想气体的内能仅是温度的函数,即
\[U=f(T)\]在这里,我们不知道“$f$”具体是一个什么函数,但我们知道它存在,这也就足够我们继续前进了。这便是所谓的隐函数。隐函数的思想是极为强大的,它让我们不用完全了解这个事物就能利用它向后推导。为了与普通的函数区分,我们一般把上式写成 $U=U(T)$,但其实表达了相同的意思。
现在,我们已终于可以正式开始了。
正章一:体积功、热容与迈耶公式
想象你正在用火烧一个气球。不妨假设球内装的是一定量的理想气体,根据公式 $pV=nRT$,气球内的气体受热便会体积膨胀,直到内部压强和外部气压相等。在膨胀的过程中,气体会对气球壁做功。我们把这种功称为体积功,因为它是由气体体积变化引起;反之,其他和体积变化没关系的功就叫做非体积功。在实际中,两种功一般是共存的,但在思想实验中,为了防止麻烦,我们可以假设非体积功为 $0$。即,所有功都是体积功,这会让计算方便许多。
现在,想象我们用那种可以完全阻止任何物质穿过且坚不可摧的理想材料做了一个圆柱体封闭容器,内部装的全是理想气体。在非体积功为零的假设下,我们来加热这个容器。由于容器封闭,气体的体积变化为 $0$,体积功也自然为零。根据热力学第一定律,立刻可得
\[\Delta U=Q\]上述过程中,设系统吸收很少量的热($dQ$)时温度上升了 $dT$,将这两个量的比值定义为一个新概念,即等容热容($C_V$)。即
\[C_V=\frac{dQ}{dT}\]结合两式,得
\[C_V=\frac{dU}{dT}\]由于对于理想气体,$U=U(T)$,所以 $C_V$ 表示了该函数在各个温度下的斜率。对于一般的理想气体,有 $C_V=C_V(T)$,即 $C_V$ 仅与 $T$ 有关;但是,我们可以假设一种极端理想气体,其 $C_V$ 是一个常数,而与 $T$ 无关。我们在后面会用到这样的假设。
现在,我们把容器改装一下,把圆柱容器的盖子掀了,然后在其中放入一个理想的活塞。这个活塞无限薄,与容器壁之间没有摩擦,同样可以阻隔任何物质,且坚不可摧。现在我们加热容器底部,内部的理想气体原本与外界气压 $p_{ex}$ 相同,受热后气体膨胀推动活塞,最终平衡时内外气压再次相等。设活塞被向上推动了 $\Delta l$ 的距离,如下图所示,那么在这个过程中系统对环境做了多少功呢?
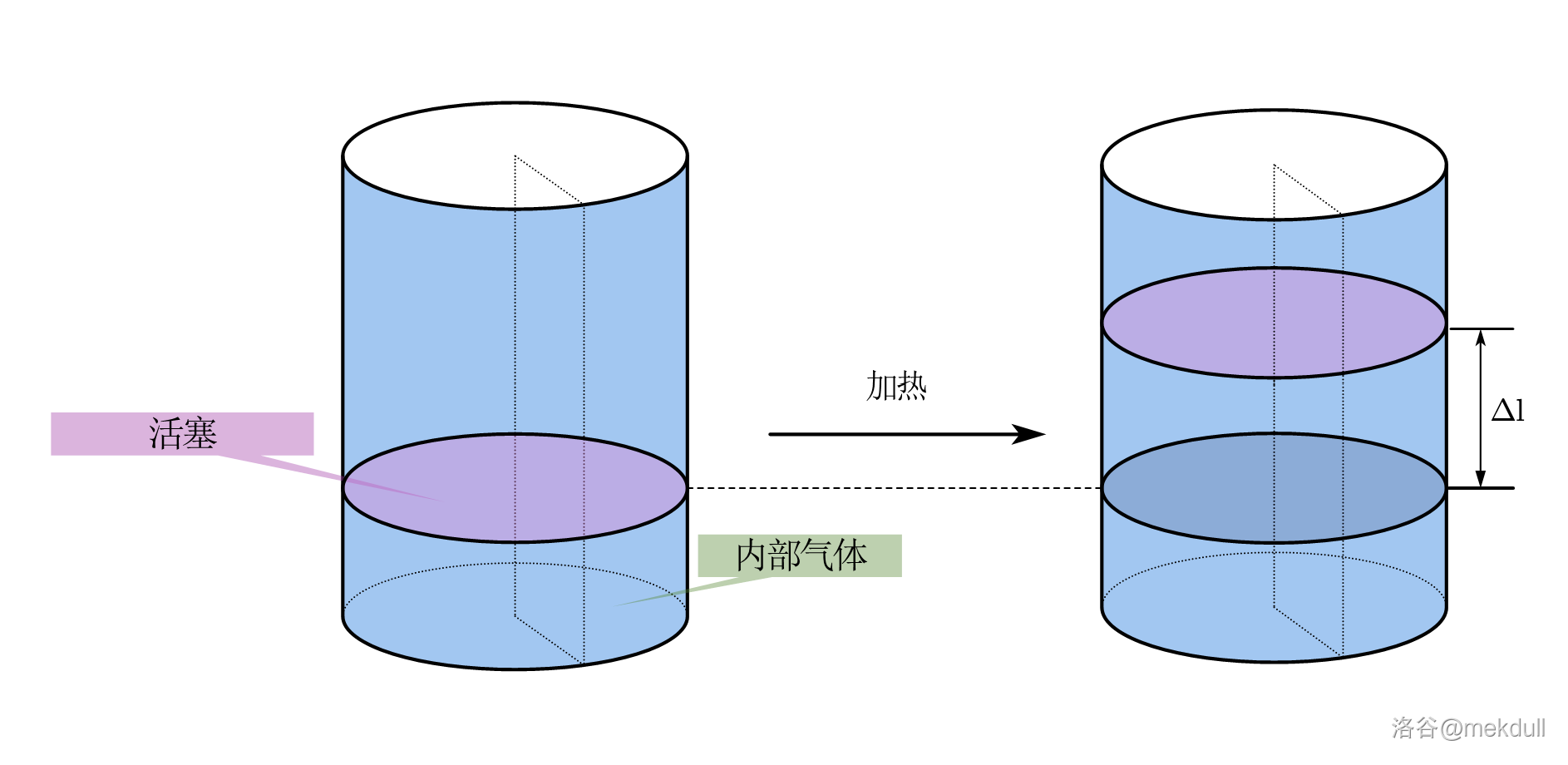
你可能会觉得这没法算,因为我们并不知道内部气体升高了多少温度,进而算不出内部气体在膨胀过程中气压的变化。但是,内部气体始终是在反抗外界恒定的气压,外界气体对这个活塞做了多少负功,也就意味着内部气体对活塞做了多少正功。定义活塞移动方向为正方向(由于只有两个方向,所以不用向量计算也没关系),则有:
\[W=-W_{ex}=-F·(-\Delta l)=p_{ex}S\Delta l\]注意到,气体膨胀的体积 $\Delta V=S\Delta l$,故有
\[W=p_{ex}\Delta V\]设气体吸收了 $Q_{p}$ 的热,那么由热力学第一定律(同样要假设非体积功为零),有
\[\Delta U=Q_{p}-W=Q_{p}-p_{ex}\Delta V=Q_{p}-p_{ex}(V_2-V_1)\]此处之所以是减 $W$,是因为此处是系统对环境做功,而热力学第一定律方程中的 $W$ 是环境对系统做的功,故需要取负值。$V_2$ 表示加热膨胀之后内部气体的体积,而 $V_1$ 表示加热之前内部气体体积。
设 $p_1$ 表示加热之前内部气体气压,而 $p_2$ 表示加热膨胀完之后内部气体气压($U_1,U_2$ 同理)。由于这两个时候系统都处于平衡态,所以有 $p_1=p_2=p_{ex}$,那么
\[\Delta U=U_2-U_1=Q_p-p_2V_2+p_1V_1\]整理得 $(U_2+p_2V_2)-(U_1+p_1V_1)=Q_{p}$
我们引入新定义:$H\equiv U+pV$,那么上式可以写成
\[H_2-H_1=Q_p\]$H$ 就是通常说的焓。实际上,你找不到一个明确的可观测的性质对应系统的焓,它只是一个人为组合出来的东西。但从上式我们可以知道,在外界压力不变的过程中(一般把这种过程称为等压过程),焓变等于吸收的热。
在上述过程中,假设系统的焓变化了一个很小的数值 $\partial H$,而系统的温度对应变化了 $\partial T$,将这两个量的比值定义为一个新概念,即等压热容($C_p$)。即:
\[C_p=(\frac{\partial H}{\partial T})_p\]这里不得不用偏微分的形式,但其实很好理解。“$\partial$”表示的意思也是微小变化,右下角的“$p$”表示是在 $p$ 不变的条件下。有了两个热容的概念,很容易得到:
\[C_p-C_v=(\frac{\partial H}{\partial T})_p-\frac{dU}{dT}\]即
\[C_p-C_v=(\frac{\partial(U+pV)}{\partial T})_p-\frac{dU}{dT}=(\frac{\partial U}{\partial T})_p+p(\frac{\partial V}{\partial T})_p-\frac{dU}{dT}\]注意到对于理想气体,$U$ 只与 $T$ 有关,而与 $p$ 无关,所以
\[(\frac{\partial U}{\partial T})_p=\frac{dU}{dT}\]代入上式,得
\[C_p-C_v=p(\frac{\partial V}{\partial T})_p\]对理想气体状态方程 $pV=nRT$ 变形得 $V=nRT/p$,代入上式得
\[C_p-C_v=p(\frac{\partial(\frac{nRT}{p})}{\partial T})_p=p~·\frac{1}{p}~·nR(\frac{\partial T}{\partial T})_p=nR\]恭喜你,获得了热力学中的一把圣剑——迈耶公式($Mayer’s~formula$)。这个公式推导起来并不难,但是不论在纸上还是现实中都有十足的威力。我们再把它写一遍:
\[C_p-C_v=nR\]对于一定量理想气体,其等压热容和等容热容的差是定值,为 $nR$。这里还要说一嘴,等压热容和等容热容是物质的固有属性,虽然我们是从等容过程和等压过程中把它们推导出来的,但是这两个概念并不依赖于这些过程而存在。也就是说,对于理想气体的任何过程,迈耶公式是普适的。迈耶公式也告诉我们,对于等容热容是定值的一定量极端理想气体来说,其等压热容也是定值。接下来,就让我们用这把“圣剑”,去开辟新的热力学天地吧。
正章二:绝热可逆方程
让我们把刚才设想的那种材料升个级,让它不仅能完全阻隔任何物质,还可以完全阻隔任何热。此时,我们便可以用这种材料构建一个绝热系统,即这个系统不会与环境进行任何热交换。还是刚才的那个带活塞(当然,活塞也得附加一条完全阻隔任何热)的圆柱形容器,只不过这次我们要求把盖子盖上,且在活塞上面的部分抽真空(可以假设这部分无限大,所以不用担心碰到顶),活塞下面的部分充入一定量理想气体。为了使其平衡,我们还要再活塞上放置几个砝码,如下图:
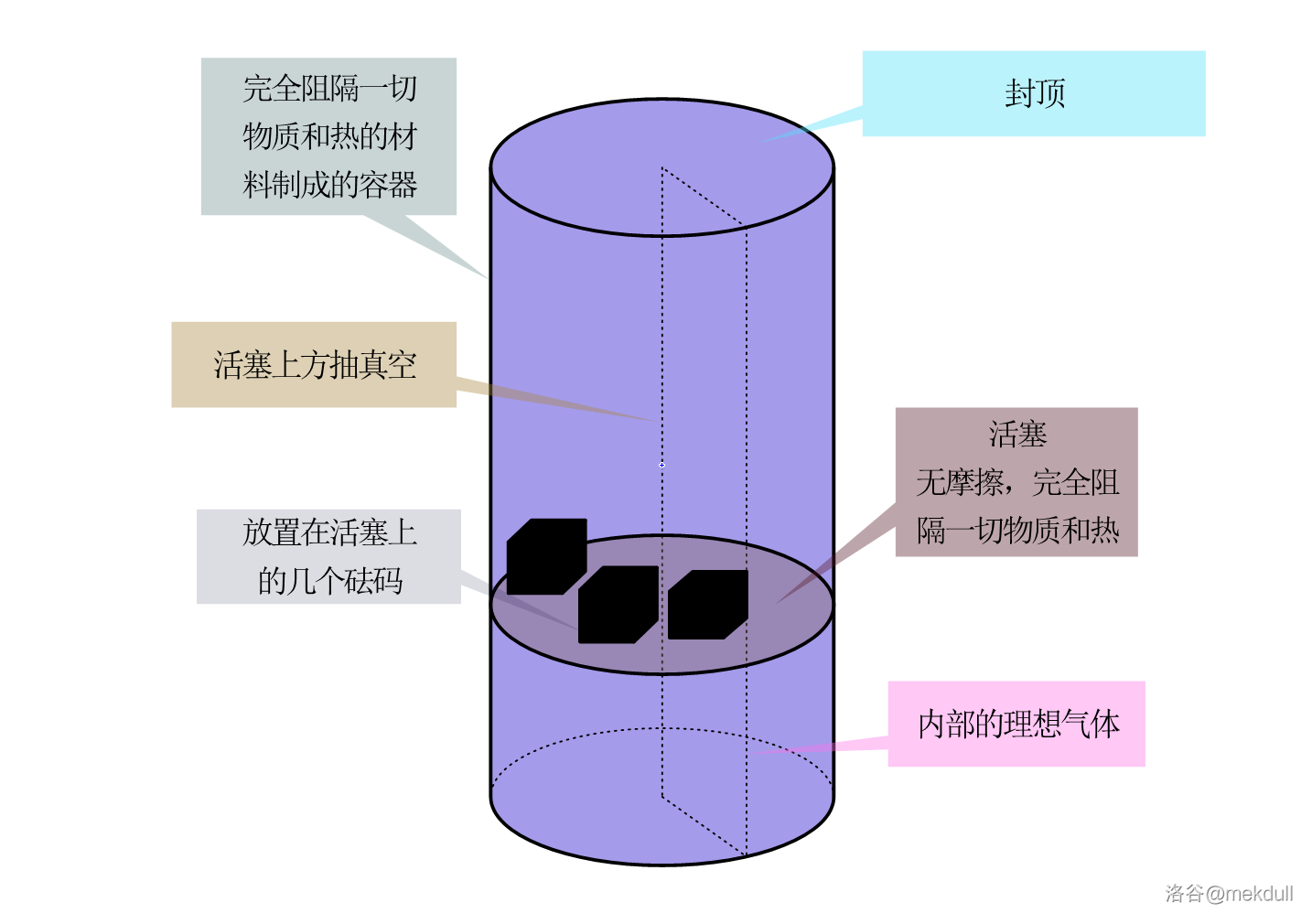
现在整个系统处于平衡状态。此时我们拿掉 $1$ 个砝码,剩下砝码的总质量为 $m$,活塞内的气体膨胀了 $\Delta V$ 的体积,压力减小,最终再次达到平衡。假设非体积功为零,那么此过程中,内部气体对外做了多少功?
和上一章中同样的方法,内部气体反抗 $mg$ 的恒定外压(也就是 $mg/S$ 的恒定压强,$S$ 是活塞的面积)膨胀,则有
\[W=\frac{mg}{S}(V_2-V_1)=\frac{mg}{S}\Delta V\]现在,我们希望将整个系统还原回初始状态。你可能会觉得这很简单,只需要把拿掉的这个砝码重新放上去就行了。但真的是这样吗?我们可以证明,这个系统再也回不去了,无论你加多少个质量为多少的砝码,做多少功,都不可能还原这个系统。
证明非常简单。假设初始状态内部气体的气压为 $p_1$,体积为 $V_1$,温度为 $T_1$,我们就可以用数对 $(P_1,V_1,T_1)$ 表示其状态。同样的,可以设重新平衡后气体状态为 $(P_2,V_2,T_2)$。由于是绝热过程,即 $Q=0$,根据热力学第一定律,有 $\Delta U=-W$,即内部气体损失了 $W$ 的内能。对于理想气体来说,内能仅是温度的函数,所以假设我们可以通过放置总质量为 $M$ 的砝码复原系统,那么“复原”的过程一定也得向内部气体做 $W$ 的功,否则平衡后温度就不会是 $T_1$ 了;复原之后内部气体体积从 $V_2$ 变回 $V_1$,则复原过程中体积变化应为 $V_2-V_1$。用同样的算法计算这个功,可以得到
\[W=\frac{(m+M)g}{S}(V_2-V_1)\]结合上两式,可以得到:
\[\frac{mg}{S}(V_2-V_1)=\frac{(m+M)g}{S}(V_2-V_1)\]化简得
\[\frac{m}{m+M}=1\]如果上式要成立,那么一定有 $M=0$。但等等,$M=0$ 不就相当于什么都不操作吗?在什么都不操作的情况下系统怎么会“自动”复原呢?所以直接矛盾,原假设不成立。也就是说,我们没有任何办法可以复原这个系统。我们一般把这样“不可能复原”的绝热过程称为绝热不可逆过程。(当然,此处“不可能复原”建立在环境不变的情况下,所以你把整个装置拆掉重建并称其为“复原”不在考虑的范围内)
那么,有没有可逆的绝热过程呢?理想状态下是有的。想象活塞上放的不是砝码,而是细沙。每粒细沙的质量极轻,记为 $dm$;每次拿掉一粒细沙,等平衡之后再拿下一粒,直到你满意为止。当 $dm\to 0$ 时,这就是一个绝热可逆过程了。完事之后,你只需要把细沙一粒一粒再放上去,就可以复原这个系统。
现在,还是上面这个细沙的理想模型,我们把内部的气体换成一定量极端理想气体。我们来关注这一过程中拿掉某一粒沙子前后,设拿掉之后剩余沙子质量为 $m$,拿掉这粒沙子前后体积变化为 $\Delta V$,则用上面的算法,有
\[dW=\frac{mg}{S}dV\]由于每次拿完沙子就会建立一次内外压的平衡,所以内部气压 $p$ 就等于 $mg/S$。结合克拉伯龙方程,得
\[dW=\frac{nRT}{V}dV\]又由于热力学第一定律,可知 $dU=-dW$。结合等容热容的定义可知
\[dW=-C_vdT\]联立上二式,得
\[\frac{nRT}{V}dV=-C_vdT\]移项后积分,可得
\[\int_{V_1}^{V_2}\frac{nR}{V}dV=-\int_{T_1}^{T_2}\frac{C_v}{T}dT\]上式中,$V_1,V_2$ 分别表示该过程初始和终了状态内部气体的体积,$T_1,T_2$ 同理。该积分积出来后可得
\[nR~\text{ln}\frac{V_2}{V_1}=C_V~\text{ln}\frac{T_1}{T_2}\]代入迈耶公式 $C_p-C_v=nR$,移项化简后得到
\[(\frac{C_p}{C_v}-1)~\text{ln}\frac{V_2}{V_1}=\text{ln}\frac{T_1}{T_2}\]给 $C_p/C_v$ 赋予一个新名字:热容比,用符号 $\gamma$ 表示。即使对于实际气体,由于热容比的值随温度变化不大,所以经常被看作定值(当然温度变化不能太离谱)。而对于我们的极端理想气体,其 $C_v$ 是定值,$C_p$ 是定值,$\gamma$ 自然也是个定值。由此我们得到:
\[(\gamma-1)~\text{ln}\frac{V_2}{V_1}=\text{ln}\frac{T_1}{T_2}\]即 $T_1V_1^{\gamma-1}=T_2V_2^{\gamma-1}~(1)$。再次代入克拉伯龙方程,可得
\[p_1V_1^{\gamma}=p_2V_2^{\gamma}~(2)\] \[T_1^{\gamma}p_1^{1-\gamma}=T_2^{\gamma}p_2^{1-\gamma}~(3)\]上述 $(1),(2),(3)$ 三式就是大名鼎鼎的绝热可逆方程,它对于极端理想气体的绝热可逆过程是永远成立的。实际工程中由于这三个公式由于偏差不大,也被广泛使用。我们的热力学圣剑现在又镀上了一层金,并很快就会大显它的身手。
在本章的最后,我们给出对于普遍的可逆过程和不可逆过程的定义。即,如果系统由状态 $A$ 变成状态 $B$ 后可以回到状态 $A$,且消除该过程中对环境产生的一切影响(我们称之为可以完全复原),那么这个过程是一个可逆过程。反之,如果不能完全复原,那么就是不可逆过程。关于这两种过程,有一个重要的公理:一切自发过程都是不可逆过程。这是人类总结生活经验和自然现象得出的,在后面关于熵增定律的讨论中,我们会意识到这条规律到底多么冷酷无情。
正章三:卡诺循环
卡诺循环源自 $1824$ 年,年轻的法国工程师萨迪·卡诺($N.~L.~S.~Carnot$)对热机效率问题的探寻。所谓热机,就是把热转变成功的机器,而热机效率 $η$ 就是热机对外做的功与吸收的热量之比,即
\[η=\frac{-W}{Q}\]在瓦特($J.~Watt$)改良了蒸汽机之后,如何提高热机效率就成为了工程师们非常关注的问题,而卡诺就想用数学方法推导出热机效率的理论最大值。于是,他在脑海中设计了一种理想的热机,也就是今天所说的卡诺热机。
卡诺热机的本体结构很简单,就是一个普通的气缸,内部有一个活塞,而活塞连接着一个飞轮。气缸被活塞分成两部分,上半部分抽真空,下半部分装入一定量的极端理想气体。活塞上方的压力完全来自于飞轮系统本身的重力,我们在此假设外面的人可以随时操作飞轮,从而改变其压力到任何一个值;飞轮系统本身可以无损耗地输出内部气体对外做的所有功,且整个系统完全无摩擦。活塞和气缸内壁可以完全阻隔任何物质和热,气缸底部可以阻隔任何物质,但允许热量交换;配套的还有一个无限大的热源(温度为 $T_1$)和一个无限大的冷源(温度为 $T_2$):
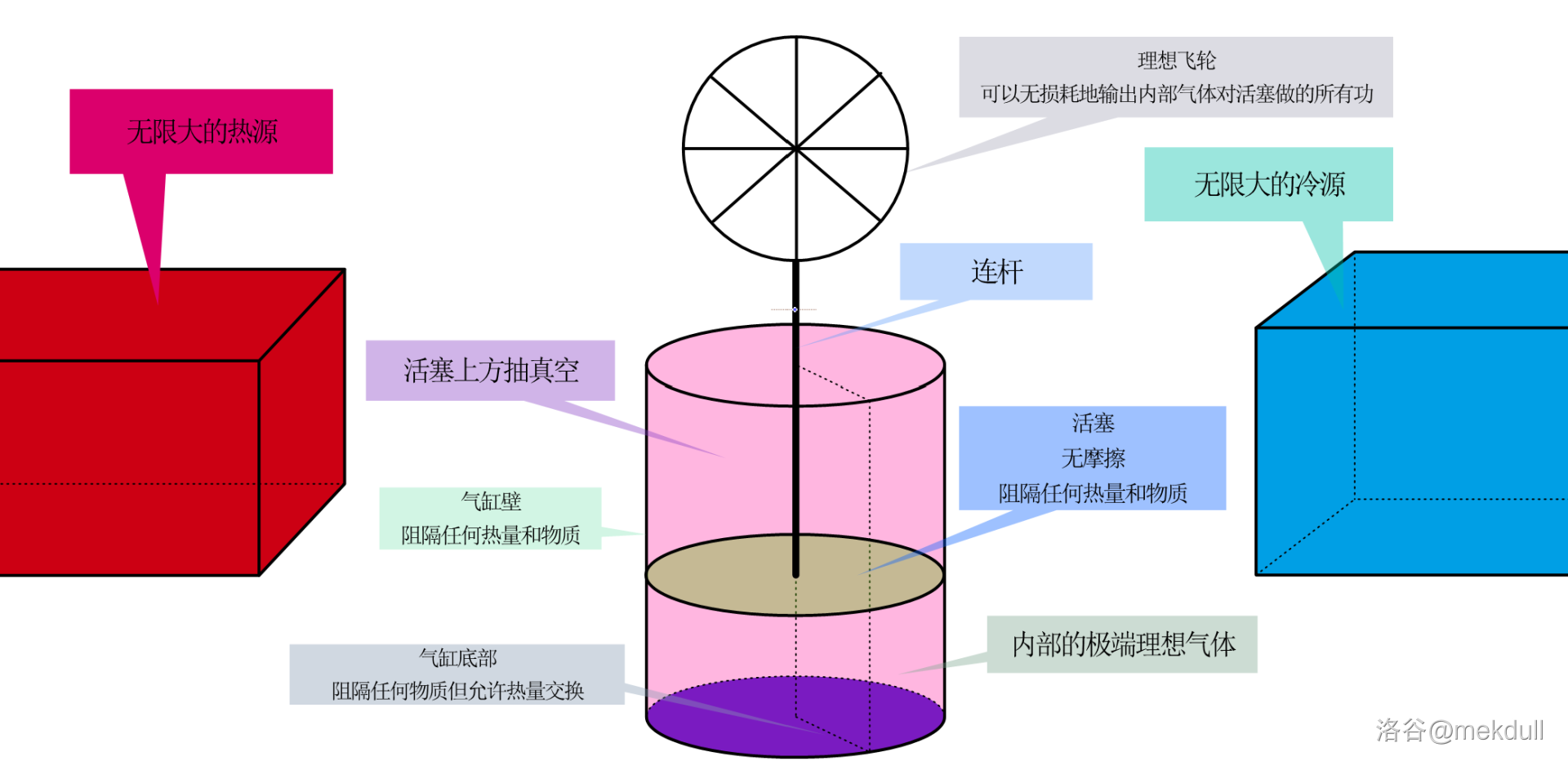
理想状态下,内部气体的初始温度 $T_0$ 略小于 $T_1$,仅相差一个无穷小量。现在,卡诺用这台机器设计了一个过程,循环进行以下四个步骤:
- 气缸底部与无限大热源接触,不断调节压力使内部气体等温可逆膨胀;
- 撤去无限大热源,不断调节压力使内部气体绝热可逆膨胀,直到气体温度下降到 $T_3$,$T_3$ 仅比 $T_2$ 大一个无穷小量;
- 气缸底部与无限大冷源接触,不断调节压力使内部气体被等温可逆压缩;
- 撤去无限大冷源,不断调节压力使内部气体被绝热可逆压缩,直到气体温度回到 $T_0$,进行下一轮循环。
(注:由于热源和冷源都是无限大的,所以不论与内部气体之间交换了多少热,其本身的温度不会改变;之所以要使 $T_0$ 与 $T_1$ 之间相差一个无穷小量,是为了使热源能够不断地把热传递给内部气体,同时内部气体温度不会变化;$T_3$ 与 $T_2$ 之间同理,都是为了构筑“等温”这个条件。)
由于卡诺热机是理想模型,所以我们不用管具体该怎样操作。我们就假设有一个超人般的操作员,每时每刻都可以用精湛的技术操作压力到任何一个值,不论我们要求的压力变化如何细微都没有任何问题。总之,他可以保证整个过程完全可逆。
我们为这个循环画一张图,以内部气体体积为横坐标,内部气体气压为纵坐标。由于第 $1$ 步和第 $3$ 步是等温可逆过程,根据 $pV=nRT$,可知其图像是反比例函数的一部分;第 $2$ 步与第 $4$ 步是绝热可逆过程,根据绝热可逆方程式 $(2)$ 可知 $p_1V_1^{\gamma}=p_2V_2^{\gamma}$。故有下图:
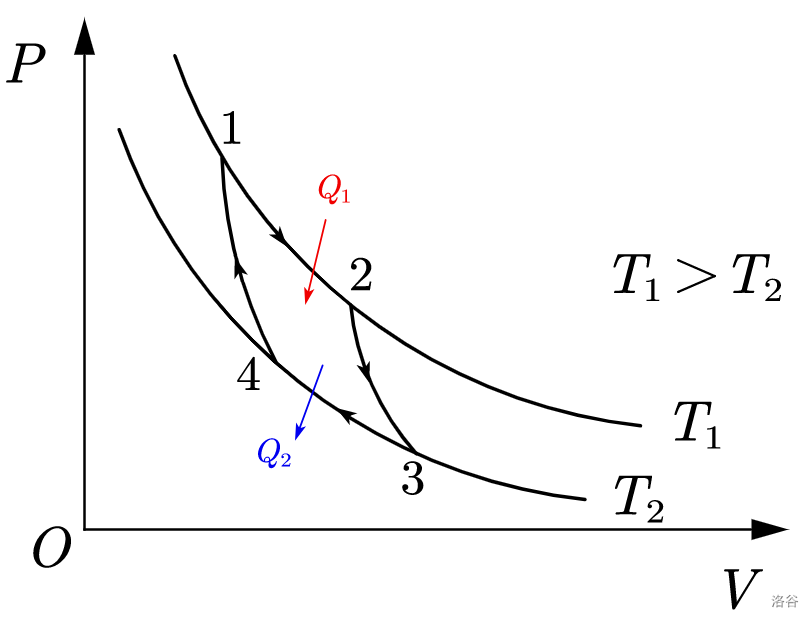
图中,黑色箭头表示循环过程的方向,$Q_1$ 是系统从热源吸收的热,$Q_2$ 是系统传递给冷源的热,数字标出的点表示该步骤执行前内部气体的状态。由于步骤 $1,3$ 是等温可逆过程,而理想气体的内能仅是温度的函数,所以有
\[\Delta U_1=\Delta U_3=0\]由热力学第一定律,得
\[Q_1=-W_1,Q_2=-W_3\]注意此处 $Q_1$ 是正数,因为是系统从环境中吸热;$Q_2$ 是负数,因为是系统向环境放热。由于 $dW=pdV$,且 $1,3$ 步骤都是可逆的,所以积分可得
\[-W_1=\int^{V_2}_{V_1}pdV=nRT_1ln(\frac{V_2}{V_1})\] \[-W_3=\int^{V_4}_{V_3}pdV=nRT_2ln(\frac{V_4}{V_3})\]由于内部气体在经历了一个循环过后回到了原点,所以 $\Delta U_{总}=0$;根据热力学第一定律,有
\[-W=Q_{总}=Q_1+Q_2=-W_1-W_3\]一个循环过程中热机从热源吸收的热为 $Q_1$,所以根据热机效率的定义式,可得
\[η=\frac{-W}{Q_1}=\frac{-W_1-W_3}{Q_1}=\frac{-W_1-W_3}{-W_1}=1+\frac{W_3}{W_1}\]代入 $W_1,W_3$ 的表达式,得
\[η=1+\frac{T_2ln(\frac{V_4}{V_3})}{T_1ln(\frac{V_2}{V_1})}\]由于 $2,4$ 是绝热可逆过程,所以根据绝热可逆方程式 $(1)$,有
\[T_1V_2^{\gamma-1}=T_2V_3^{\gamma-1}\] \[T_1V_1^{\gamma-1}=T_2V_4^{\gamma-1}\]两式相除,可得
\[(\frac{V_2}{V_1})^{\gamma-1}=(\frac{V_3}{V_4})^{\gamma-1}\]进而有 $V_2/V_1=V_3/V_4$。设 $V_2/V_1=V_3/V_4=k$,代入 $η$ 的表达式,有
\[η=1+\frac{T_2ln(1/k)}{T_1ln(k)}=1-\frac{T_2ln(k)}{T_1ln(k)}=1-\frac{T_2}{T_1}\]上面这个式子非常重要,所以我们再把它写一遍:
\[η=1-\frac{T_2}{T_1}\]这个式子在告诉我们什么?它告诉我们,即便是如此理想化的卡诺热机,效率也不可能达到 $100\%$,因为 $T_2/T_1$ 总是大于 $0$;只有 $T_2\to 0$ 或者 $T_1\to \infty$ ,才有 $η\to 1$。需要注意,这篇文章中所有的温度都采用热力学温标,单位为开尔文($K$),而不是摄氏度($^{\circ}C$),因此 $T_2\to 0$ 是指 $T_2$ 趋向于绝对零度。虽然当时热力学第三定律还没有建立,但卡诺已经相信温度有一个不可达到的最低值,进而相信卡诺热机的效率不可能达到 $1$。
至此,卡诺已经完成了思维的闭环,是时候把成果总结并公布了。他在论文中写下了下面这两句话:
- 卡诺热机的效率可以用 $1-T_2/T_1$ 来表示,故卡诺热机的效率达不到 $100\%$;
- 任何热机的效率都不可能超过使用同样温度热源的卡诺热机的效率。
这就是大名鼎鼎的卡诺定理,而我们的主角,也即将被这个重要的定律推上舞台。
正章四:热力学第二定律与熵
在卡诺刚提出这个定律时使用的仍是古老的热质说思想,因此在热质说式微以后,卡诺定律也理所应当地被众人所怀疑。我们上面看到的一连串推导,都是 $1850$ 年前后克劳修斯等人的工作。现在,距离重新证明其实还差一步,也就是卡诺定律的第二句话。如何证明“任何热机的效率都不可能超过使用同样温度热源的卡诺热机?”
克劳修斯意识到,必须再引入一条坚实的、不证自明的公理才能继续前进。这条公理就是:热不可能自发地从低温物体传到高温物体,而不引起其他变化。我们今天一般把它称为热力学第二定律。由于热力学第二定律有很多种等价的表述方法,为了区分,我们一般把上面这句话叫做克劳修斯表述。和第一定律一样,它是一条公理,直接来自于人们对自然现象的总结与归纳。现在,让我们来完成卡诺定律证明的最后一步。
克劳修斯假设了一台名为“$r$”的热机,它的效率大于使用同温热源的卡诺热机 $R$。设 $r$ 一个循环过程做功为 $W$,从热源吸收的热为 $q_1$;$R$ 一个循环过程做功也为 $W$,但需要从热源吸收 $Q_1$ 的热。根据热机效率的定义,有
\[\frac{W}{q_1}=η_r>η_R=\frac{W}{Q_1}\]进而 $Q_1>q_1$。设 $r$ 向冷源放热 $q_2$,$R$ 向冷源放热为 $Q_2$,根据热力学第一定律,有
\[W=q_1-q_2=Q_1-Q_2\]进而 $Q_2>q_2$。现在看看我们的卡诺热机 $R$,它有一个特点,就是他是可逆的。卡诺热机的每个步骤都是可逆的,因此我们可以倒过来,把每个步骤中的“膨胀”改为“压缩”,“压缩”改为“膨胀”——这其实只需要让操作员反过来操作压力就行了,卡诺热机本身的结构不需要改动。这个反过来的 $R$ 唤作 $R’$,可以对比一下它们每个循环干的事:
$R:$ 从热源吸收 $Q_1$ 的热,向冷源放 $Q_2$ 的热,做 $W$ 的功;
$R’:$ 向热源放 $Q_1$ 的热,从冷源吸收 $Q_2$ 的热,消耗 $W$ 的功。
注意,$R’$ 并没有违反热力学第二定律,它虽然实现了把热从低温传到高温,但需要消耗功。现实生活中类似的机械,比如夏天制冷的空调,都是需要消耗大量功才能把热量从低温处传到高温处。但或许已经有读者发现不对劲了:如果我用 $r$ 做的功,去驱动 $R’$,会怎么样?
$r$ 每个循环从热源吸收 $q_1$ 的热,驱动 $R’$ 向热源放 $Q_1$ 的热;$r$ 向冷源放 $q_2$ 的热,但 $R’$ 也会从冷源吸收 $Q_2$ 的热。总的来说,这个 $r-R’$ 一体机每个循环会向热源放 $Q_1-q_1$ 的热,从冷源吸收 $Q_2-q_2$ 的热。由于 $Q_1>q_1,Q_2>q_2$,而 $r$ 做的功和 $R’$ 消耗的功刚好一样。热力学第二定律被违反了,因为这个 $r-R’$ 一体机在不需要外界供给任何功的情况下就把热量从低温物体带到了高温物体。唯一的解释是,$r$ 是专属于上帝的机器,实际上根本不可能存在。也就是说,不可能有热机的效率超过使用同样温度热源的卡诺热机。卡诺定律由此得证。
但是,克劳修斯认为这还不够。他希望拓展卡诺定律到更广阔的领域,超越热机系统的局限。
他注意到可以通过以下方式改写卡诺定律:
\[η=\frac{W}{Q_1}=\frac{Q_1+Q_2}{Q_1}\leq η_{卡}=1-\frac{T_2}{T_1}\Rightarrow\frac{Q_1}{T_1}+\frac{Q_2}{T_2}\leq 0\]我们可以把上式称为卡诺定律的变形式。这个式子中一定蕴含了很多奥秘,克劳修斯心想。他看了看一旁的 $p-V$ 图,突然灵光乍现。上式只有在所有循环都是卡诺循环时才取等号,那么这 $n$ 个紧挨在一起的卡诺循环,在 $p-V$ 图上会怎样表现呢?
为了简化问题,我们先考虑 $n=2$ 的情况。可以看到,两个循环之间有一部分重叠,进而相互抵消(用虚线表示),最终留下的是一条封闭的折线:(此处借用一下@東雲正樹大佬的图)
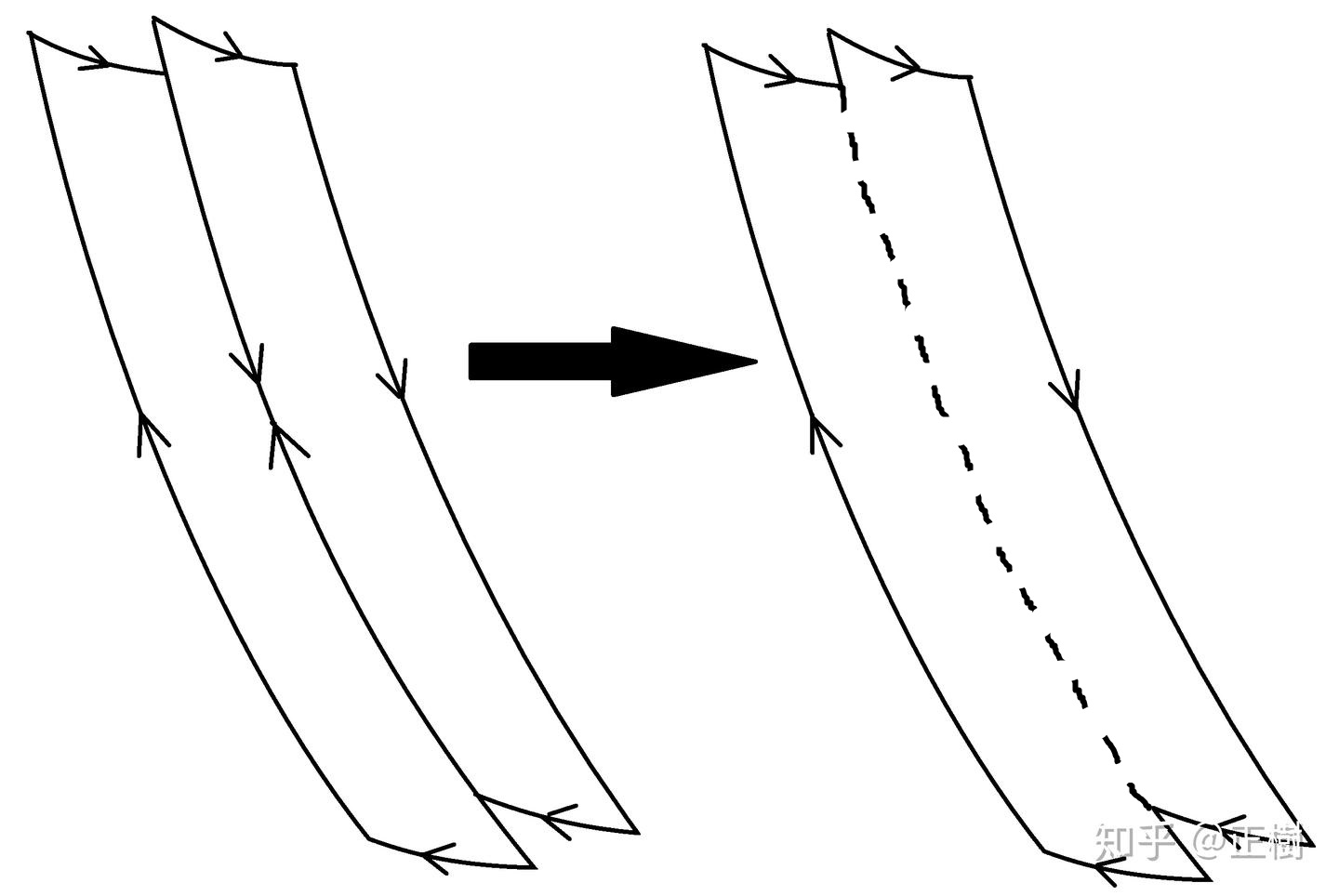
注意看这条虚线,它和两侧与它弧度相同的两条线在 $p-V$ 图中被称为绝热线,因为它们对应了卡诺循环中的绝热可逆过程;上下的几条较短的线则是等温线,代表了卡诺循环中的等温可逆过程。
我们知道,任何可逆的循环过程,无论有多少个步骤,都一定可以表示为 $p-V$ 图上的一段封闭曲线。这很好理解,$p-V$ 图在本质上是散点图,图上每个点都表示系统的一个平衡状态,而可逆过程时时刻刻都是平衡的,因此表示可逆过程的曲线必定连续;又因为是一个循环,所以曲线会首尾相接。反之,我们刚才说过,不可逆元过程只有两个平衡态,在 $p-V$ 图上表示为两个不重合的点,而一个不可逆过程必定至少包含一个不可逆元过程,所以其曲线一定不连续。
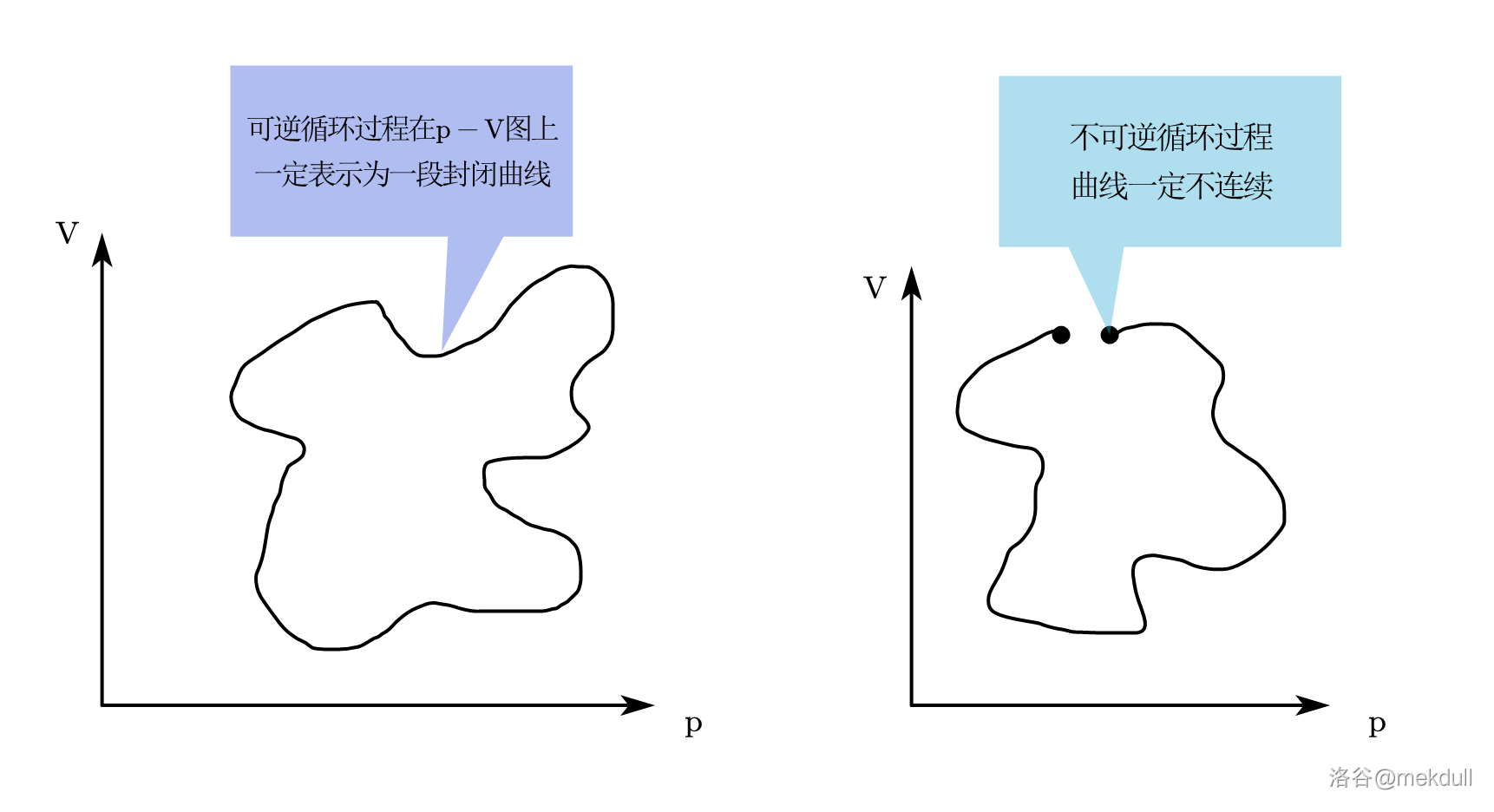
现在,我们尝试用 $n$ 条绝热线(下图中蓝线)去截这段封闭曲线(下图中粗黑线)。在每两条截线之间,我们再画上下两条与原封闭曲线相交的等温线(下图中细黑线):
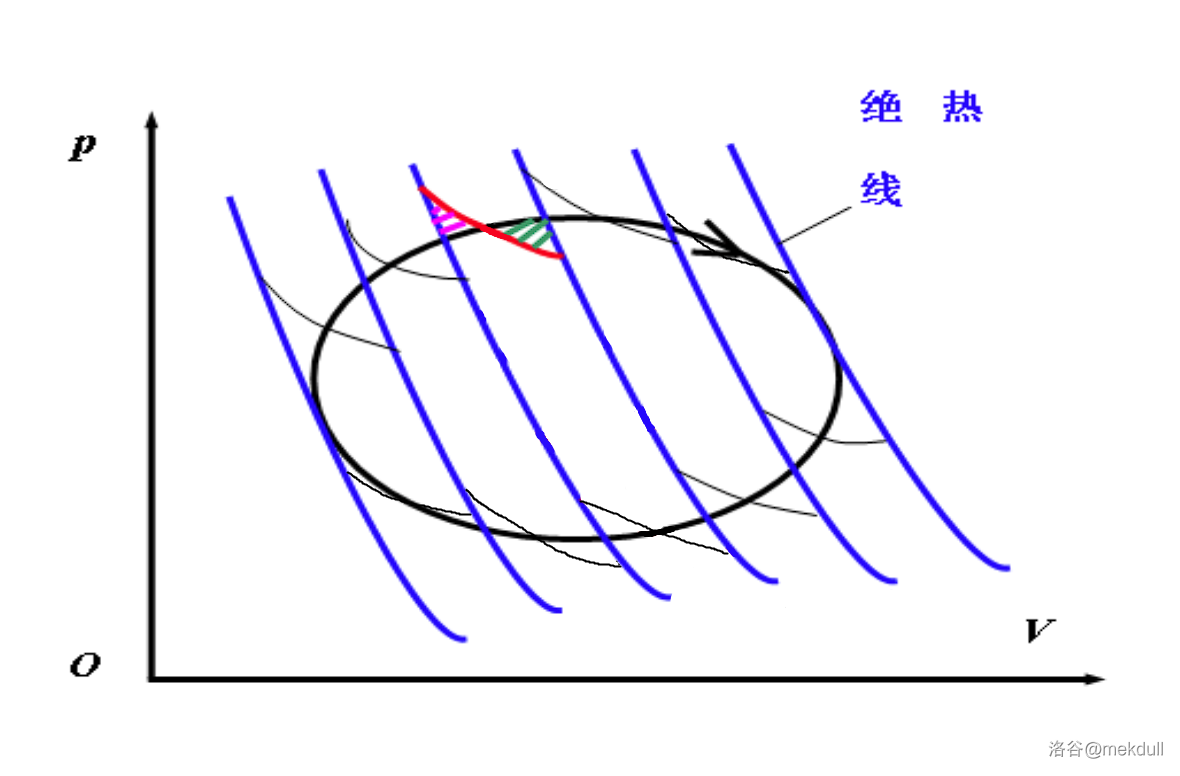
以其中一条等温线(上图中红线)为例,它的两侧产生了两个封闭的曲边三角形。通过选取合适的等温线,我们可以使得这两块图形的面积(上图中粉色和绿色部分)相等。其他等温线的选取遵守同样的规则。用这些新画出来的线可以构筑一个新的循环,如下图中黄线所示:
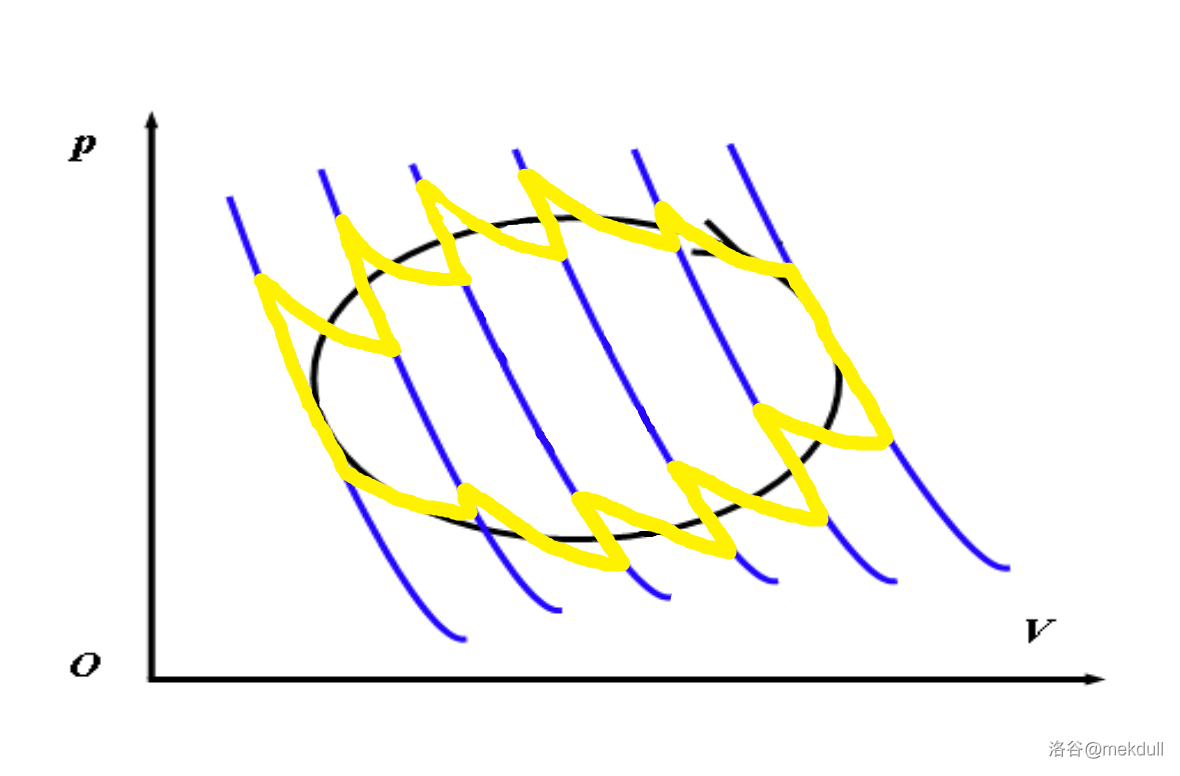
注意到,这个新循环就是 $n-1$ 个紧挨在一起的卡诺循环,且由于对等温线的选取规则,这段新曲线在图中围出的面积与原循环相等。注意到,随着 $n$ 变大,原曲线与新曲线会越来越接近。上图中 $n$ 只有 $6$,二者相差还比较大,直观上感觉就是新曲线的“刺”比较多;下图中取了 $n=12$,可以感觉到“刺”变得不那么尖锐了,新曲线和原曲线也更加接近了:
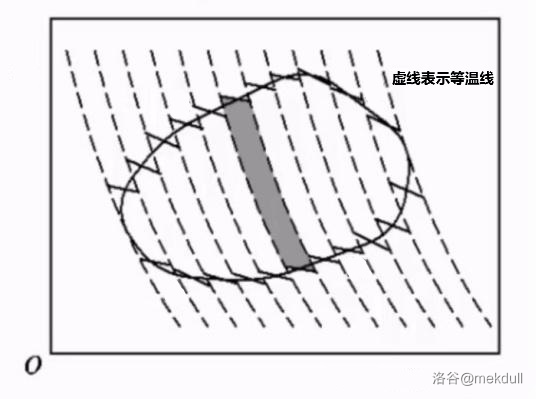
当 $n\to \infty$ 时,新曲线与原曲线重合,即原来的可逆循环过程被等价为了无数个挨在一起的微小卡诺循环。接着,克劳修斯写下了一个式子:
\[\oint\frac{\delta Q}{T}\]式中,$\oint$ 是环积分符号,表示这是对一个循环过程进行积分;$\delta$ 是不恰当微分的符号(也有人把这个符号写成 $\mathrm{d}\kern{-4.3pt}\bar{\small\phantom{q}}$ 或者 $\mathrm{d}\hspace{-7pt}-$,但用知乎的 $Latex$ 编辑器打出这两个东西很麻烦),意在表示对 $\delta Q$ 直接积分是没有结果的,因为它与路径有关。想要完全理解不恰当微分需要一些高深的数学知识,如果你此前没有学过,可以直接把 $\delta$ 看成普通微分符号 $d$,至少在这篇文章里并不会有什么问题。分母上的 $T$ 则表示环境温度,而不是系统温度。这个式子的值,称为这个循环过程的热温商。
对于一个卡诺循环来说,其第一步和第三步是等温过程,环境温度 $T$ 不变;第二步与第四步是绝热过程,$\delta Q=0$。结合卡诺定律的变形式,有
\[\oint_{卡}\frac{\delta Q}{T}=\int_{1}\frac{\delta Q}{T}+\int_{2}\frac{\delta Q}{T}+\int_{3}\frac{\delta Q}{T}+\int_{4}\frac{\delta Q}{T}=\frac{Q_1}{T_1}+0+\frac{Q_2}{T_2}+0=0\]即卡诺循环的热温商为零。而对于一个普通的可逆循环过程,上面已经证明,可以看成是无数个挨在一起微型的卡诺循环的组合,所以有:
\[\oint_{可逆}\frac{\delta Q}{T}=\lim_{n \to \infty}\sum_{i=1}^{n}\oint_{卡}\frac{\delta Q}{T}=0\]这便是克劳修斯恒等式。不过,它只告诉了我们可逆循环过程的热温商一定为零,而不关心更普遍的不可逆循环过程。但没事,克劳修斯的工作还没有结束。可以证明,一切涉及不可逆过程的热机效率一定小于卡诺热机的效率,进而把刚才那套逻辑重走一遍,就能得到
\[\oint_{不可逆过程}\frac{\delta Q}{T}<0\]篇幅所限,主要是因为比较重复,上式的详细证明过程在此略去(读者如果感兴趣可以尝试自证)。只是,克劳修斯的发力还没结束。假设在 $p-V$ 图(轴没有画出)中有 $A,B$ 两点,路径 $\text{I}$ 是从 $A\to B$ 的可逆过程,路径 $\text{II}$ 是从 $B\to A$ 的可逆过程,如下图:
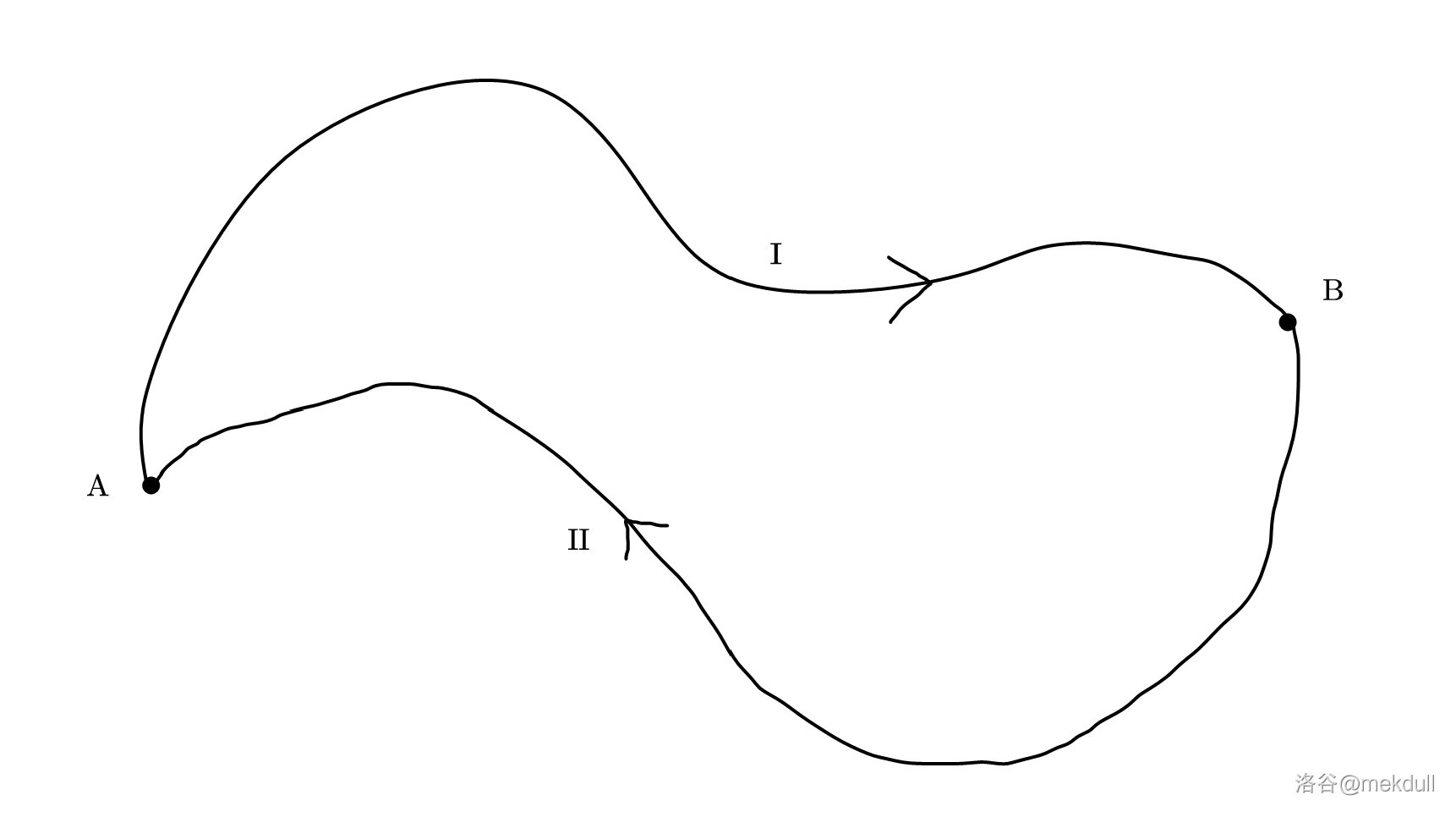
那么两条路径构成一个可逆循环过程,即有
\[\int_{A}^{B}\frac{\delta Q}{T}(\text{I})+\int_{B}^{A}\frac{\delta Q}{T}(\text{II})=\oint\frac{\delta Q}{T}= 0\]移项得
\[\int_{A}^{B}\frac{\delta Q}{T}(\text{I})=-\int_{B}^{A}\frac{\delta Q}{T}(\text{II})\]进而根据积分的性质,有
\[\int_{A}^{B}\frac{\delta Q}{T}(\text{I})=\int_{A}^{B}\frac{\delta Q}{T}(\text{II})\]对于 $A,B$ 间的任意两条可逆路径 $\text{I,II}$,上式都成立。也就是说,可逆过程的热温商只与初始和终末状态有关,而与路径无关。克劳修斯将其定义为一个新的物理量,并赋予了它一个如雷贯耳的名字——
熵($Entropy$)